Matrix multiplication

33 languages

• Article
• Talk
• Read
• Edit
• View history

Tools

From Wikipedia, the free encyclopedia

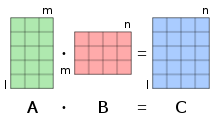
For matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. The result matrix has the number of rows of the first and the number of columns of the second matrix.

In mathematics, particularly in linear algebra, matrix multiplication is a binary operation that produces a matrix from two matrices. For matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. The resulting matrix, known as the matrix product, has the number of rows of the first and the number of columns of the second matrix. The product of matrices A and B is denoted as AB.^[1]

Matrix multiplication was first described by the French mathematician Jacques Philippe Marie Binet in 1812,^[2] to represent the composition of linear maps that are represented by matrices. Matrix multiplication is thus a basic tool of linear algebra, and as such has numerous applications in many areas of mathematics, as well as in applied mathematics, statistics, physics, economics, and engineering.^[3][4] Computing matrix products is a central operation in all computational applications of linear algebra.

Notation[edit]

This article will use the following notational conventions: matrices are represented by capital letters in bold, e.g. A; vectors in lowercase bold, e.g. a; and entries of vectors and matrices are italic (they are numbers from a field), e.g. A and a. Index notation is often the clearest way to express definitions, and is used as standard in the literature. The entry in row i, column j of matrix A is indicated by (A)_ij, A_ij or a_ij. In contrast, a single subscript, e.g. A₁, A₂, is used to select a matrix (not a matrix entry) from a collection of matrices.